Anotações sobre Estruturas de Dados

1 Estruturas de dados e análise de complexidade

DEFINIÇÃO: ESTRUTURA DE DADOS

Todo o dado atômico é aquele no qual o conjunto de dados manipulados é indivisível, ou seja, você trata-os como sendo um único valor. Por sua vez, dados complexos são aqueles cujos elementos do conjunto de valores podem ser decompostos em partes mais simples. Se um dado pode ser dividido, isso significa que ele apresenta algum tipo de organização estruturada e, portanto, é chamado de dado estruturado, o qual faz parte de uma estrutura de dados.

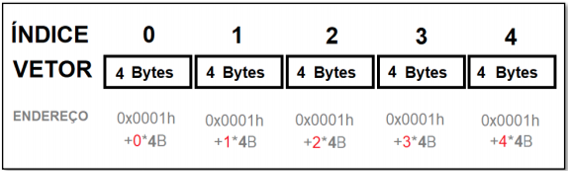
Estruturas de dados homogêneas são aquelas que manipulam um só tipo de dado. Você já deve ter tido contato com esse tipo de dado ao longo de seus estudos anteriores em programação. Vetores são estruturas homogêneas de dados. Um vetor será sempre unidimensional. Se desejarmos trabalhar com duas dimensões, trabalhamos com matrizes e, mais do que duas dimensões denominamos de tensores. Vetor é um tipo de estrutura de dados linear que necessita de somente um índice para indexação dos endereços dos elementos. O vetor contém um número fixo de células. Cada célula armazenará um único valor, sendo todos estes valores do mesmo tipo de dados. Quando declaramos uma estrutura de vetor, na memória do programa ele é inicializado (alocado) a partir da primeira posição (endereço da primeira célula). Cada outra célula, a partir da segunda, possui um endereço de referência relativoà primeira célula endereçada. Esse endereço é calculado considerando a posição da primeira célula, acrescido do tamanho em bytes de cada célula, tamanho que depende do tipo de dado armazenado no vetor.

Chamamos isto de alocação sequencial.

Uma matriz é uma estrutura de dados homogênea, linear, com alocação sequencial e bidimensional. Para cada uma das dimensões da matriz, é necessário utilizar um índice diferente. Também podemos afirmar que cada dimensão de uma matriz é na verdade um vetor. Em outras palavras, uma matriz é um vetor de vetor. Considerando nosso exemplo bidimensional, nossa matriz é composta, portanto, por dois vetores. Podemos generalizar a forma de cálculo de cada posição na memória de uma matriz pela Equação 2:𝐸𝑛𝑑𝑒𝑟𝑒ç𝑜𝑖,𝑗 = 𝐸𝑛𝑑𝑒𝑟𝑒ç𝑜0,0 + (Í𝑛𝑑𝑖𝑐𝑒𝑙𝑖𝑛ℎ𝑎 ∗ 𝐶 ∗ 𝑇𝑎𝑚𝑎𝑛ℎ𝑜𝐵𝑦𝑡𝑒𝑠)+ (í𝑛𝑑𝑖𝑐𝑒𝑐𝑜𝑙𝑢𝑛𝑎 ∗ 𝑇𝑎𝑚𝑎𝑛ℎ𝑜𝐵𝑦𝑡𝑒𝑠).

Estruturas de dados heterogêneas, também conhecidas como registros (ou structs na linguagem de programação C).

ANÁLISE DE COMPLEXIDADE DE ALGORITMOS

Ao analisarmos o desempenho de um algoritmo, existem dois parâmetros que precisam ser observados:

• Tempo de execução – quando tempo um código levou para ser executado;
• Uso de memória volátil – a quantidade de espaço ocupado na memória principal do computador; Acerca do tempo de execução, um fator bastante relevante nesse parâmetro é o tamanho do conjunto de dados de entrada.

O custo em tempo de execução de um algoritmo é o tempo que ele demora para encerrar a sua execução. Podemos medir de forma empírica esse tempo de execução. As linguagens de programação, e até o próprio compilador, fornecem recursos e ferramentas capazes de mensurar esses tempos.

Como forma de abstrair nossa análise do hardware e de softwares que são alheios ao nosso desenvolvimento, podemos encontrar matematicamente o custo de um algoritmo, encontrando uma equação que descreve o seu comportamento em relação ao desempenho do algoritmo. Encontrar esse custo é prever os recursos que o algoritmo utilizará. A função custo T(n) de um algoritmo qualquer pode ser dada como: 𝑇(𝑛) = 𝑇𝑡𝑒𝑚𝑝𝑜 + 𝑇𝑒𝑠𝑝𝑎ç𝑜.

Para encontrarmos esse custo em tempo de execução, consideramos as seguintes restrições em nossas análises:

• Nossos códigos rodarão em um, e somente um, microprocessador por vez;· Não existirão operações concorrentes, somente sequenciais;
• Consideraremos que todas as instruções do programa contêm um custo unitário, fixo e constante.

Uma instrução será uma operação ou manipulação simples realizada pelo programa, como: atribuição de valores, acesso a valores de variáveis, comparação de valores e operações aritméticas básicas.

Perceba que o pior caso e o melhor caso resultam em duas funções de custo diferentes.

ANÁLISE ASSINTÓTICA DE ALGORITMOS

Nesse tipo de análise, encontraremos uma curva de tendência aproximada do desempenho de um algoritmo. A análise baseia-se na extrapolação do conjunto de dados de entrada, fazendo-os tenderem ao infinito e permitindo que negligenciemos alguns termos de nossas equações. Em outras palavras, descartamos de nossas equações os termos que crescem lentamente à medida que nosso conjunto de dados de entrada tende ao infinito.

Para obtermos o comportamento assintótico de qualquer função, mantemos somente o termo de maior grau (maior crescimento) da equação, negligenciando todos os outros, inclusive o coeficiente multiplicador do termo de maior grau.

a. GRANDE-O (BIG-O):

• Define o comportamento assintótico superior;
• É o pior caso de um algoritmo;
• Mais instruções sendo executadas.

b. GRANDE-ÔMEGA:

• Define o comportamento assintótico inferior;
• É o melhor caso do algoritmo (caso ótimo);
• Menos instruções sendo executadas.

c. GRANDE-TETA:

• Define o comportamento assintótico firme;
• Caso médio de um algoritmo.
• É o comportamento considerando a grande maioria dos casos.

Vamos trabalhar com o a notação Big-O, que é a notação mais empregada em análises de algoritmos e nos diz que um código nunca será pior do que a situação mostrada nesta notação, podendo, no entanto, ser melhor, dependendo do conjunto de dados de entrada.

RECURSIVIDADE

A recursão é o processo de definição de algo em termos de si mesmo. Um algoritmo recursivo é aquele que utiliza a si próprio para atingir algum objetivo, ou obter algum resultado. Em programação, a recursividade está presente quando uma função realiza chamadas a si mesma.

Percebemos o interessante desempenho da função recursiva, porém, como o algoritmo recursivo está abrindo muitas instâncias de uma mesma função, e para cada nova instância temos suas variáveis locais sendo alocadas novamente, isso significa um aumento do uso de memória desse programa. Portanto, deve-se tomar cuidado com a possibilidade de estouro da pilha de memória em aplicações recursivas.

2 Algoritmos de ordenação e busca

Algoritmos de ordenação

Cada dado pertencente a uma coleção de dados deve conter um número de registro (chave). Esta chave serve para identificar de forma única um dado dentro de toda a coleção. Todos os dados que estão vinculados a uma chave são chamados de dado satélite.

Uma maneira de otimizarmos um algoritmo é, em vez de permutarmos toda a coleção de dados satélite de cada entrada de dados, vincular uma variável do tipo ponteiro a cada registro. Assim, permutamos e organizamos somente estes ponteiros, não precisando realocar todo o conjunto de dados satélite em memória, reduzindo o consumo de recursos, aumentando a eficiência o desempenho do processo.

Um algoritmo de ordenação é um método que descreve como é possível colocar, em uma ordem específica, um conjunto de dados qualquer.

Algoritmo de ordenação por troca (bubble sort)

Apesar de ser o algoritmo de ordenação mais simples, e frequentemente o mais utilizado para o entendimento do processo de ordenação, este é um algoritmo computacionalmente muito caro e muito ineficiente. Notadamente porque emprega dois laços de repetição aninhados.

Dentro do laço interno, existe um teste condicional que compara o valor de uma posição do vetor com o próximo valor, efetuando uma troca entre eles, caso necessário, utilizando uma variável auxiliar.

Conforme vimos, o algoritmo proposto continua testando se os valores estão posicionados corretamente, mesmo quando o vetor já está ordenado. O que constitui desperdício de recursos computacionais.

Podemos solucionar este problema e otimizar o desempenho de nosso código, bem como trocar nosso laço externo do tipo para por um laço enquanto(ou mesmo um repita). Neste laço de enquanto, continuaremos fazendo nossa contagem que vai até o tamanho do vetor, exatamente como antes, mas também acrescentamos outra condição, uma variável do tipo lógico com dois estados, inicializada com nível lógico baixo e que se mantém neste valor ao menos que exista uma troca. Portanto, enquanto houver trocas, seu valor será de nível alto. Quando o nível lógico volta a ser baixo, o laço encerrará precocemente, economizando nas iterações desnecessárias.

A complexidade assintótica para o pior caso do método de ordenação por troca, tanto para a versão original quanto para a versão aprimorada será igual.

Lembrando que um laço de repetição só tem impacto no desempenho assintótico do algoritmo caso estejam aninhados, ou seja, um inserido no outro. Percebemos a existência de dois laços de repetição aninhados. Portanto, temos para Big-O: 0𝐵𝑢𝑏𝑏𝑙𝑒𝑆𝑜𝑟𝑡(𝑛²).

Analogamente, a versão aprimorada também tem dois laços aninhados, resultando na mesma complexidade para o pior caso. Se a complexidade é a mesma, por que então utilizamos a versão aprimorada? Porque para as situações em que o pior caso não ocorrerá, a nova versão se sairá melhor.

Algoritmo de Ordenação por intercalação (merge sort)

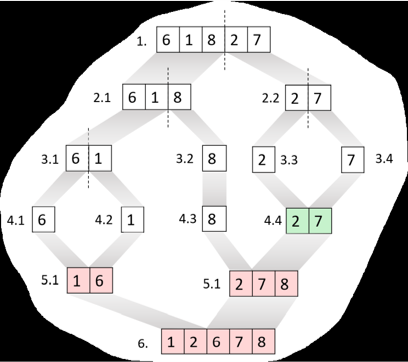
Este algoritmo de ordenação trabalha com a divisão da estrutura de dados em partes menores, empregando uma técnica chamada de dividir para conquistar. Para tal, empregam-se funções recursivas para a realização desta tarefa.

O processo do merge sort consiste em dividir uma estrutura de dados de tamanho n (um vetor por exemplo) em n partes de tamanho unitário. Ou seja, o conjunto de dados inicial vai sendo dividido ao meio até que restem somente partes indivisíveis. Quando duas partes subsequentes atingirem tamanho um, elas realizam o processo chamado de intercalação. De forma simples, podemos entender a intercalação como a ordenação (crescente ou decrescente) seguida da agregação das partes para formarem um vetor maior.

Para encontrarmos a complexidade assintótica para o pior caso do merge sort, precisamos, primeiro, analisar a complexidade individual de ambas funções propostas. Temos a função merge sendo chamada recursivamente. A complexidade assintótica para o pior caso de uma função recursiva será 𝑂(𝑙𝑜𝑔(𝑛)).

A função merge também faz a chamada de outra função, a intercala. Esta função opera de forma iterativa. Não temos laços encadeados, portanto a complexidade para um único laço será 𝑂(𝑛).

Como a função intercala está inserida na função merge, para encontrar a complexidade assintótica Big-Oh resultante, multiplicamos a complexidade de ambas funções. A complexidade para o pior do merge sort é superior em tempo de execução se comparado com o bubble sort. 0𝑀𝑒𝑟𝑔𝑒𝑆𝑜𝑟𝑡(𝑛. log(𝑛))

Algoritmo de ordenação rápida (quick sort)

O quick sort é bastante empregado em virtude de sua eficiência e facilidade de implementação. A ordenação rápida trabalha com o conceito de pivô, em que um elemento do conjunto de dados é selecionado para servir como referência de comparação para os outros valores.

A ordenação ocorre quando o método divide a estrutura de dados em duas partes, semelhante ao merge sort, porém esta divisão não necessariamente ocorre no ponto central do vetor.

Diferentemente do merge sort, o objetivo deste algoritmo não é quebrar o vetor no menor tamanho possível, mas sim dividi-lo para encontrar o elemento pivô. Para uma ordenação crescente, os elementos à esquerda do pivô devem sempre ser menores do que ele, e os à direita, maiores que o pivô. O algoritmo é aplicado de forma recursiva nas partes divididas até que a estrutura esteja ordenada.

A complexidade final para o quick sort será 𝑂𝑄𝑢𝑖𝑐𝑘𝑆𝑜𝑟𝑡(𝑛2)

Algoritmos de busca

Algoritmos de busca servem para localizar um valor específico em um conjunto de dados. Assim como apresentado nos algoritmos de ordenação, a quantidade de algoritmos de busca disponível é diversa, e cada um destes algoritmos apresentará vantagens e desvantagens, além de desempenhos distintos e, consequentemente, aplicações diferentes.

Busca sequencial

• A busca sequencial tem como fim introduzir o assunto de algoritmos de busca. A proposta do algoritmo de busca sequencial consiste em realizar uma busca em um conjunto de dados (ordenado ou não), empregando ao menos um laço de repetição que fará a varredura do conjunto de dados (lógica iterativa). Para cada iteração, temos uma comparação simples entre o elemento a ser localizado e cada elemento deste conjunto de dados.
• A complexidade assintótica para o tempo de execução da busca sequencial, com vetor ordenado ou não, será sempre 𝑂(𝑛).

Busca binária

• A busca binária que trabalha com o conceito de dividir um conjunto de dados sempre ao meio e comparar o ponto central com o valor buscado é o conhecido processo de dividir para conquistar. Se este ponto central for menor ou maior que o valor buscado, a região de busca do vetor é limitada para o ramo esquerdo ou direto do conjunto de dados. Com esta proposta, a busca binária é capaz de atingir seu objetivo mais rapidamente e, ainda, trabalhar com recursividade, tornando o método mais eficiente se comparado ao sequencial.
• Uma característica importante é que a busca binária só funciona com conjuntos de dados já ordenados, caso contrário, a verificação feita com o ponto central não seria possível. Portanto, se o conjunto de dados não estiver ordenado, ele primeiro precisa ser ordenado para depois ser buscado.
• A busca binária apresenta como complexidade assintótica 𝑂(𝑙𝑜𝑔𝑛).

3 Listas, pilhas e filas

Conceito de listas encadeadas

Nem todas as estruturas de dados são sequenciais. Existem estruturas de dados com alocação não sequencial. Em estruturas de dados com alocação não sequencial, cada dado (ou conjunto de dados) pode estar posicionado em qualquer parte da memória destinada a um programa em execução.

Além dos dados úteis, cada elemento da lista ainda precisa manter pelo menos um endereço armazenado. Esse endereço corresponderá ao endereço do próximo elemento da lista. Dessa forma, cada elemento da lista sabe onde o próximo está e todos estão conectados (virtualmente) por meio desses endereços, ou ponteiros, armazenados.

Para uma lista, o conceito de índice é inexistente. Em uma lista, cada elemento contém o endereço do próximo elemento. Portanto, somente o elemento atual conhece o subsequente. Assim, a única forma de acessarmos, por exemplo, o terceiro elemento dessa lista seria iniciarmos no primeiro elemento e, por meio do acesso aos endereços para os próximos elementos, passarmos de um elemento para o seguinte até atingirmos o elemento desejado. Esse tipo de lista é chamado de encadeado por esse motivo, já que os elementos estão encadeados por meio do endereço do elemento seguinte.

Uma das grandes vantagens do uso de listas encadeadas está na possibilidade de alocação dinâmica de memória e no dinamismo de manipulação dos dados dessa lista, o que torna fáceis a inserção e a remoção de novos elementos.

Dentre as desvantagens das listas está o desempenho para acesso aos dados.

As listas podem ser homogêneas ou heterogêneas e armazenar qualquer tipo de dado.

Lista simplesmente encadeada (linked list)

Cada elemento dela aponta e conhece somente o próximo elemento da lista. Para tal, cada nó necessita ter um único ponteiro, com o endereço do próximo elemento. Em programação, podemos representar cada elemento da lista encadeada como sendo um registro. Esse registro conterá todos os dados que se deseja armazenar, sejam quais forem seus tipos, e também um ponteiro. Esse ponteiro conterá o endereço para o próximo elemento da lista. O tipo desse ponteiro deverá ser igual ao do registro criado.

A lista encadeada simples pode ser classificada em dois tipos: as não circulares e as circulares.

O primeiro elemento da lista é chamado de início ou de head (cabeça) da lista. Esse primeiro elemento é o único que sempre será conhecido pelo programa que está manipulando uma determinada lista. Todos os outros dados da lista são descobertos à medida que os elementos da lista vão sendo acessados.

Em uma lista simples não circular, o último elemento não apontará para nada (ponteiro nulo). De uma forma diferente, a lista simples circular difere da não circular somente pelo ponteiro do último nó. Esse ponteiro, ao invés de apontar para o nulo, irá apontar para o primeiro elemento da lista, fechando um círculo.

Inserindo um novo elemento no início da lista encadeada simples não circular

Passo 1: alocar o novo elemento na memória. Perceba que alocá-lo na memória ainda não significa inseri-lo na lista. Nesse momento, ele ainda está fora da lista.

Passo 2: fazer o ponteiro do novo elemento apontar para o head.

Passo 3: transformar o novo elemento no novo head da lista.

Inserindo um novo elemento no fim da lista encadeada simples não circular

Passo 1: alocar o novo elemento na memória. Perceba que alocá-lo na memória ainda não significa inseri-lo na lista. Nesse momento ele ainda está fora da lista.

Passo 2: realizar uma varredura, usando um laço de repetição e começando no head, até localizar um elemento que aponte para o nulo. Esse elemento será o último e a inserção do novo elemento ocorrerá após ele.

Passo 3: fazer esse último elemento apontar para o nosso novo valor. O novo valor, como será então o último, irá apontar para o nulo.

Inserindo um novo elemento no meio da lista encadeada simples não circular

Passo 1: alocar o novo elemento na memória. Perceba que alocá-lo na memória ainda não significa inseri-lo na lista. Nesse momento, ele ainda está fora da lista.

Passo 2: realizar uma varredura, usando um laço de repetição e começando no head até localizar a posição desejada.

Passo 3: fazer o elemento da posição anterior apontar para o novo elemento e fazer o novo elemento apontar o antigo da posição desejada.

Lista duplamente encadeada (doubly linked list)

Uma lista duplamente encadeada é assim chamada pois cada elemento dela aponta e conhece o próximo elemento da lista, bem como o elemento imediatamente anterior a ele na lista. Para tal, cada nó necessita ter dois ponteiros (anterior e próximo).

Em programação, podemos representar cada elemento da lista encadeada como sendo um registro. Esse registro conterá todos os dados que se deseja armazenar, sejam quais forem seus tipos, e também os dois ponteiros. Um ponteiro conterá o endereço para o próximo elemento da lista e o outro, o endereço para retornar ao elemento anterior. O tipo desse ponteiro deverá ser igual ao do registro criado.

A lista encadeada dupla pode ser classificada em dois tipos: as não circulares e as circulares. Em uma lista dupla não circular, o último elemento apontará para o nulo. De uma forma diferente, a lista dupla circular difere da não circular somente pelo ponteiro próximo do último nó. Esse ponteiro, ao invés de apontar para o nulo, irá apontar de volta para o primeiro elemento da lista, fechando um círculo novamente.

Inserindo um novo elemento no início da lista encadeada dupla

Passo 1: alocar o novo elemento na memória. Perceba que alocá-lo na memória ainda não significa inseri-lo na lista. Nesse momento, ele ainda está fora da lista.

Passo 2: fazer o ponteiro próximo do novo elemento apontar para o head. Fazer o ponteiro anterior ao novo elemento apontar para o nulo. Fazer o ponteiro anterior ao head apontar para o novo elemento.

Passo 3: transformar o novo elemento no novo head da lista.

Inserindo um novo elemento no fim da lista encadeada dupla

Passo 1: alocar o novo elemento na memória. Perceba que alocá-lo na memória ainda não significa inseri-lo na lista. Nesse momento, ele ainda está fora da lista.

Passo 2: realizar uma varredura na lista existente, iniciando no head, até localizar o elemento com ponteiro próximo nulo (último elemento).

Passo 3: fazer o elemento encontrado, com ponteiro próximo nulo, apontar para o novo elemento. Fazer o ponteiro anterior ao novo elemento apontar para o último elemento. Fazer o ponteiro próximo do novo elemento apontar para o nulo.

Inserindo um novo elemento no meio da lista encadeada dupla

Passo 1: alocar o novo elemento na memória. Perceba que alocá-lo na memória ainda não significa inseri-lo na lista. Nesse momento, ele ainda está fora da lista.

Passo 2: executar uma varredura na lista existente, iniciando no head, até localizar a posição desejada (posição 2).

Passo 3: utilizando uma variável de lista auxiliar, fazer a inserção do elemento no meio. O elemento da posição 1 irá apontar para o novo elemento, com seu ponteiro próximo. O antigo elemento da posição 2 apontará, com seu anterior, também para o novo elemento. O novo elemento irá apontar, com seu ponteiro anterior, para o 9 e, com seu ponteiro próximo, para o 5.

Pilha (stack)

Uma pilha se comporta seguindo a regra chamada: o primeiro que entra é o último que sai. Em inglês, essa regra é chamada de first in last out (Filo).

Em programação, podemos criar uma estrutura de dados que também funciona com esse princípio que acaba de ser explicado. Essa estrutura pode ser construída tanto com vetores quanto com listas encadeadas. Ambas funcionarão da mesma maneira detalhada anteriormente. As diferenças estarão nas características da estrutura de dados, características essas intrínsecas a elas. Vetores funcionarão com alocação sequencial da memória e tempo de acesso aos dados constante. Listas funcionarão com alocação dinâmica e tempo de acesso às informações 𝑂(𝑛).

Dentre algumas aplicações comuns de pilhas está a própria técnica de programação chamada recursividade, já bastante desenvolvida nas aulas anteriores. Cada instância de uma função recursiva aberta é tratada como um novo elemento inserido na pilha. Esse novo elemento precisa ser resolvido para então desempilharmos os demais elementos e assim termos acesso ao elemento (outra função) que está abaixo, na pilha.

Top, único elemento sempre conhecido globalmente pelo programa.

Inserindo um novo elemento na pilha (empilhando/push)

Passo 1: alocar o novo elemento na memória. Perceba que alocá-lo na memória ainda não significa inseri-lo na pilha. Nesse momento, ele ainda está fora da pilha.

Passo 2: fazer o ponteiro do novo elemento apontar para o top.

Passo 3: transformar o novo elemento no novo top da lista.

Removendo um elemento da pilha (desempilhando/pop)

Passo 1: localizar o topo da pilha.

Passo 2: transformar o elemento subsequente ao topo no novo topo.

Passo 3: liberar da memória o topo antigo, para que ele não ocupe espaço desnecessário na memória do programa.

Fila (Queue)

Uma fila se comporta seguindo a regra chamada: o primeiro que entra é o primeiro que sai. Em inglês, essa regra é chamada de first in first out (Fifo).

Em programação, podemos criar uma estrutura de dados que também funciona com esse princípio que acaba de ser explicado. Essa estrutura pode ser construída tanto com vetores quanto com listas encadeadas.

Dentre algumas aplicações comuns de filas na área de tecnologia, podemos citar o processo de fila de impressão, em uma rede. Cada arquivo que é colocado para imprimir, em uma mesma impressora, é inserido no final da fila. E o que está na frente da fila é removido (impresso) primeiro.

Inserindo um elemento na fila (queuing)

Passo 1: alocar o novo elemento na memória. Perceba que alocá-lo na memória ainda não significa inseri-lo na pilha. Nesse momento, ele ainda está fora da fila.

Passo 2: varrer a fila até encontrar o ponteiro nulo (último elemento).

Passo 3: fazer o ponteiro nulo do último elemento apontar para o novo elemento.

Removendo da fila (dequeuing)

Passo 1: localizar o head da fila.

Passo 2: transformar o elemento subsequente ao head no novo head.

Passo 3: liberar da memória o head antigo, para que ele não ocupe espaço desnecessário na memória do programa

4 Árvores

Árvore binária

A árvore binária é uma estrutura de dados não linear organizada com elementos que não estão, necessariamente, encadeados, formando ramificações e subdivisões na organização da estrutura de dados. A árvore binária apresenta algumas características distintas, mesmo se comparada a outros tipos de árvores. Analisaremos algumas dessas características e conceituaremos alguns termos próprios referentes a árvores:

· Nó raiz (root):1 nó original da árvore. Todos derivam dele;

· Nó pai: nó que dá origem (está acima) a pelo menos um outro nó;

· Nó filho: nó que deriva de um nó pai;

· Nó folha/terminal: nó que não contém filhos.

O que caracteriza uma árvore como binária é o número de ramificações de cada nó. Na árvore binária, cada nó apresenta nenhum, um ou no máximo dois nós chamados de nós filhos.

Uma árvore binária apresenta como característica a inserção de valores de forma organizada. Um modo de inserção de valores é posicionar à esquerda de um nó pai, na árvore, somente valores menores do que ele. E os valores à direita devem ser maiores que o nó pai. Desse modo, valores menores sãosempre posicionados mais à esquerda da árvore e os maiores mais à direita. Esse tipo de inserção é também conhecido como Binary Search Tree (BST, árvore de busca binária).

O objetivo de inserção na árvore é justamente facilitar a busca de dados posteriormente. Como os dados estarão colocados na árvore de uma forma organizada, saberemos que, ao percorrer as ramificações de uma árvore binária, localizaremos o valor desejado mais rapidamente pelas subdivisões.

O grau de um nó na estrutura de dados em árvore corresponde ao número de subárvores que aquele nó terá. Em uma árvore binária, o grau máximo de cada nó será dois.

Em uma árvore, conceituamos o nó raiz como sendo o nível zero da árvore. Todo novo conjunto de ramificações da árvore caracteriza mais um nível nessa árvore. Conhecendo os níveis, a altura de uma árvore será calculada ao tomarmos o maior nível dela e subtrairmos do primeiro nível (nível 0). É também possível encontrarmos a altura relativa entre dois níveis da árvore. Para isso, basta subtrairmos os valores desses níveis.

Em programação, representamos cada elemento da árvore como sendo um registro que contém todos os dados que desejamos armazenar, além de dois ponteiros. Esses ponteiros conterão os endereços para os próximos elementos da árvore, ou seja, para os nós filhos daquele elemento.

Sempre que um nó for folha, significa que ele está no nível mais alto da árvore e que, portanto, não terá filhos. Sendo assim, ambos os ponteiros serão nulos. Caso o nó não seja folha, ele sempre terá ao menos um ponteiro de endereço não nulo.

Raiz (root), único elemento sempre conhecido globalmente pelo programa.

Inserção de dados

Em uma árvore binária montada para funcionar como uma Binary Seach Tree (BST) não existem inserções no início, no meio nem no final da árvore como ocorre nas listas encadeadas. A inserção sempre é feita após um dos nós folha da árvore, seguindo a regra anteriormente explanada:

• · Dados de valores menores cujos antecessores são inseridos no ramo esquerdo da árvore;

• · Dados de valores maiores cujos antecessores são inseridos no ramo direito da árvore.

Todo novo nó inserido vira um nó folha, porque ele é sempre inserido nos níveis mais altos da árvore. Todos os nós folha podem ser facilmente identificados em uma árvore como aqueles nós cujos ponteiros (esquerdo e direito) são nulos.

Passo 1: Alocar o elemento na memória (fora da árvore);

Passo 2: Encontrar a posição deste elemento na árvore;

Passo 3: Fazer o ponteiro do nó-pai apontar para o novo elemento.

Busca de dados

Passo 1: iniciando na raiz, testamos se ela é igual, maior ou menor que o valor 2. Caso fosse igual, nossa busca já poderia ser encerrada. Porém, o valor 8 é maior que 2. Isso significa que, caso o 2 exista nessa árvore, ele estará à esquerda do 8, e, portanto, devemos seguir pelo ramo esquerdo (ponteiro esquerdo);

Passo 2: estamos no nível 1 da árvore e comparando o valor 2 com o valor 6. Novamente, verificamos se esse valor é maior, menor ou igual 2. O valor é maior do que 2. Portanto, novamente, caso o 2 exista nessa árvore, ele estará à esquerda de 6, e devemos seguir para a esquerda no próximo nível;

Passo 3: estamos no nível 2 da árvore e comparamos o valor com o 2. Nesse caso, o valor é exatamente 2, e, portanto, podemos encerrar nossa busca na árvore binária.

A busca binária delimita a região de busca sempre pela metade a cada nova tentativa, tornando possível localizar, para o pior caso assintótico, o dado em um tempo de execução O(logn).

Uma árvore binária também apresenta para BigO a mesma complexidade O(logn), também delimitando a região de busca sempre pela metade a cada novo nível da árvore. Sendo assim, a árvore binária faz para as buscas em estruturas de dados dinâmicas o equivalente ao que a busca binária faz para conjuntos de dados sequenciais.

Visualização de dados

Uma árvore binária, depois de construída, pode ser listada/consultada e apresentada em uma interface. Porém, como a árvore não apresenta sequência/ordem fixas, podemos listar seus dados de algumas formas distintas. As consultas podem ser feitas:

Em ordem: listamos os elementos iniciando pelos elementos da esquerda; depois, a raiz; e, por último, os elementos da direita. Dessa forma, os elementos listados são apresentados ordenados e de forma crescente;

Em pré-ordem: listamos os elementos iniciando pela raiz, depois listamos os elementos da esquerda, e, por fim, os elementos da direita;

Em pós-ordem: listamos os elementos iniciando pelos elementos da esquerda; depois, os da direita; e, por último, a raiz.

Árvore de Adelson-Velsky e Landis (Árvore AVL)

Uma árvore de Adelson-Velsky e Landis, também conhecida como árvore AVL, é uma árvore binária balanceada. Em uma árvore binária convencional, na medida em que temos muitas inserções de dados, podemos começar a ter algumas ramificações que se estendem muito em altura, gerando piora no desempenho do algoritmo.

Ramificações muito altas acabam dificultando o sistema de busca em uma árvore, piorando o desempenho do algoritmo em termos de tempo de execução. A árvore AVL tem como objetivo melhorar esse desempenho balanceando uma árvore binária, evitando ramos longos e gerando o maior número de ramificações binárias possíveis.

Sendo assim, a árvore AVL contém todas as características já apresentadas de uma árvore binária. A única característica adicional é que a diferença de altura entre uma subárvore direita e uma subárvore esquerda sempre deverá ser 1, 0 ou –1. Caso essa diferença resulte em outro valor, como 2 ou –2, a árvore deverá ser imediatamente balanceada (seus elementos deverão ser rearranjados) por meio de um algoritmo de balanceamento.

· Passo 1: calculamos a altura relativa daquele elemento para o lado direito da árvore. Nesse caso, pegamos o nível mais alto do lado direito daquele elemento e subtraímos do nível do elemento desejado;

· Passo 2: calculamos a altura relativa daquele elemento para o lado esquerdo da árvore. Nesse caso, pegamos o nível mais alto do lado esquerdo daquele elemento e subtraímos do nível do elemento desejado;

· Passo 3: tendo as alturas direita e esquerda calculadas, fazemos a diferença entre elas (direta menos esquerda, sempre). Se o cálculo resultar em 2 ou –2, existe um desbalanceamento e uma rotação será necessária.

Rotacionando a árvore binária

Diferença de altura de um nó	Diferença de altura entre o nó filho e o nó desbalanceado	Tipo de rotação
2	1	Simples à esquerda
2	0	Simples à esquerda
2	-1	Dupla com filho para a direita e pai para a esquerda
-2	1	Dupla com filho para a esquerda e pai para a direita
-2	0	Simples à direita
-2	-1	Simples à direita

5 Grafos

Estrutura de dados que tem a sua construção sem um padrão definido e totalmente aleatória.

Um grafo G é um conjunto de vértices conectados por meio de arestas sem uma distribuição fixa ou padronizada.

Os vértices V de um grafo são seus pontos. Cada ponto pode ser um ponto de encontro entre caminhos (rotas) de um grafo, ou, então, o vértice pode conter informações relevantes para o grafo, como dados de informações de cadastros. Tudo depende da aplicação.

As arestas E são as linhas de conexão entre os vértices. Cada aresta conecta dois vértices. Nem todo vértice precisa ter uma aresta conectada; ele pode permanecer isolado, caso o grafo assim seja construído.

Chamamos de grafo completo quando existe uma, e somente uma aresta para cada par distinto de vértices; chamamos de grafo trivial aquele que apresenta um único vértice.

Assim como tínhamos o grau de cada nó de uma árvore, em grafos também podemos encontrar o grau de cada nó de um vértice. O grau de um vértice nada mais é do que a soma de todas as arestas que incidem sobre ele.

Dentre as particularidades da construção de grafos, podemos citar as arestas múltiplas. Arestas múltiplas são aquelas que estão conectadas aos mesmos vértices.

Um laço acontece quando uma aresta contém somente um vértice ao qual se conectar, iniciando e terminando nele.

Por fim, vemos um grafo desconexo. Nesse tipo de grafo, temos pelo menos um vértice sem nenhuma aresta

Para finalizar a abordagem da teoria, precisamos entender que podemos atribuir pesos a nossas arestas. O peso da aresta representa um custo atrelado àquele caminho. Quando não indicamos nenhum peso nas arestas, assumimos que elas têm todas o mesmo valor. Quando damos um número para cada aresta, indicamos os valores no próprio desenho do grafo. Chamamos um grafo com pesos em arestas de grafo ponderado.

Representação de grafos

Podemos representar os grafos matematicamente ou graficamente. As representações matemáticas acabam por ser ideais para a implementação em um algoritmo, por exemplo, já que podem ser manipuladas da forma que o desenvolvedor necessitar.

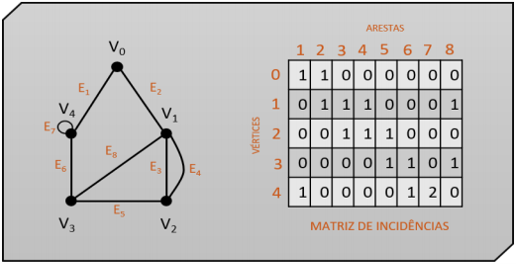
Matriz de incidências

A representação de um grafo por uma matriz de incidências consiste em criar uma matriz de dimensão VxE, em que V é o número de vértices do grafo e E, o número de arestas.

Ao analisar o grafo desenhado, devemos observar cada uma de suas arestas (colunas da matriz). Elas devem ser preenchidas segundo as possibilidades a seguir:

0, caso o vértice (linha da matriz) não faça parta da ligação;

1, caso o vértice (linha da matriz) faça parta da ligação;

2, caso aquela aresta seja do tipo laço.

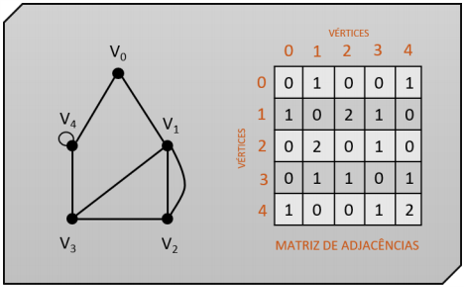
Matriz de adjacências

A representação de um grafo por uma matriz de adjacências consiste em criar uma matriz quadrada de dimensão V, em que V é o número de vértices do grafo.

Assim como na representação anterior, povoamos nossa matriz com valores 0, 1 ou 2. A análise que fazemos para preenchimento da matriz é efetuada de uma forma diferente agora. Observamos cada uma das linhas dos vértices, e preenchemos na matriz:

0, caso o outro vértice não tenha conexão com o vértice analisado;

1, caso o outro vértice tenha conexão com o vértice analisado;

2, caso o outro vértice tenha conexão com o vértice analisado e seja um laço.

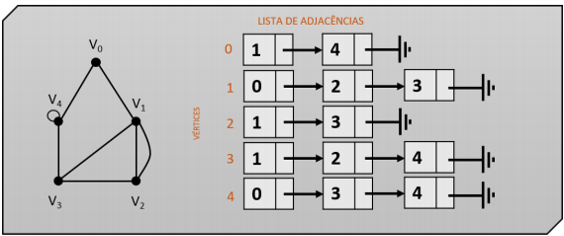
Lista de adjacências

A representação de um grafo por uma lista de adjacências é muito adotada na área de programação, pois trabalha com listas encadeadas e manipulação de ponteiros de dados.

A proposta dessa representação é criar um vetor (ou uma lista encadeada) do tamanho da quantidade de vértices existentes no grafo. Em cada posição desse vetor, teremos uma lista encadeada contendo os endereços dos vizinhos de cada vértice. Conceitualmente, vizinhos de um vértice são todos os vértices que se conectam diretamente a ele por meio de uma aresta.

Assim, teremos uma lista encadeada de vizinhos para cada posição do vetor de vértices criado. Na lista, cada vizinho apontará para outro vizinho daquele mesmo nó.

Podemos criar essa estrutura de duas formas distintas. Na primeira, declaramos um vetor de dimensão igual ao número de vértices de nosso grafo. Esse vetor será do tipo ponteiros de registros. Assim, cada posição do vetor poderá conter uma estrutura do tipo lista encadeada, armazenando o primeiro elemento dessa lista (head).

De forma alternativa, também podemos substituir o vetor por uma estrutura do tipo lista. Assim, teremos duas listas encadeadas, uma chamada de vertical, contendo os vértices e os endereços para os primeiros vizinhos, e uma lista horizontal, contendo as listas de vizinhos de cada vértice.

Algoritmo de busca em profundidade no grafo

O algoritmo de busca em profundidade, também conhecido como Depth-First Search (DFS), apresenta uma lógica intuitiva e funcional para resolver esse problema de descoberta do grafo.

A proposta desse algoritmo é partir de um vértice de origem e acessar a lista de adjacências desse vértice, ou seja, seus vizinhos. O primeiro vizinho detectado (mais adiante na lista encadeada do vértice de origem), será imediatamente acessado.

Assim, cada novo elemento ainda não descoberto é selecionado a partir das listas encadeadas de cada vértice, até que o último seja encontrado. Os elementos descobertos vão sendo empilhados e desempilhados segundo as regras de uma estrutura do tipo pilha. Ou seja, só podemos voltar ao vizinho de um nó mais abaixo na pilha se resolvermos primeiro o elemento mais acima, no topo da pilha.

Algoritmo de busca em largura no grafo

O algoritmo de busca em largura, também conhecido como Breadth-First Search (BFS), trabalha com a ideia de visitar primeiro todos os vizinhos próximos do vértice selecionado antes de pular para o próximo vértice.

Uma diferença interessante em relação à busca por profundidade é que a BFS trabalha com uma estrutura do tipo fila para indicar qual é o próximo vértice a ser acessado, enquanto na Depth-first Search (DFS) tínhamos uma estrutura de pilha.

Perceba que temos também um vetor de distâncias. Esse vetor manterá armazenada a distância de cada vértice em relação ao vértice de origem, ajudando na decisão de qual será o próximo vértice a ser visitado.

Algoritmo do caminho mínimo em grafo: Dijkstra

Esse algoritmo é o mais tradicional para realizar a tarefa de encontrar um caminho. Para realizar tal procedimento, podemos utilizar um grafo ponderado, ou seja, aquele com pesos distintos nas arestas.

Todo esse algoritmo será apresentado utilizando uma métrica aditiva. Isso significa que essa métrica encontrará a menor rota considerando o menor peso somado entre os caminhos.

Existem outros tipos de métricas. Na multiplicativa, por exemplo, o melhor caminho é encontrado calculando-se o produto dos pesos das arestas. O maior valor dentre os produtos é a melhor rota. Um exemplo dessa métrica é o limite de velocidade das estradas: quanto maior o limite, mais rápido o veículo anda, e, portanto, melhor é aquela rota/aresta.

Como trabalharemos com um grafo ponderado, precisamos adaptar nossa lista de adjacências para que o registro também armazene os pesos das arestas.

O algoritmo do caminho mínimo precisa calcular as menores rotas de um vértice para todos os outros. Portanto, um vetor com distâncias fica armazenado. Nesse vetor, todas as rotas iniciam com um valor infinito, ou seja, como se o caminho de um vértice até o outro não fosse conhecido. À medida que os trajetos vão sendo calculados, os pesos das rotas são alterados.

6 Hashs

O objetivo da hash é construir uma estrutura de dados capaz de obter tempo de acesso constante às informações contidas nela, independentemente do tamanho do conjunto de dados.

O vetor contendo os valores-chave é denominado de tabela hashing. Para cada palavra-chave, podemos ter a quantidade que necessitarmos de dados cadastrados referentes aquela chave, dados estes chamados de dados satélites.

Tabelas hashing armazenam palavras-chave que servem para acessar dados satélite. Essas palavras-chave são armazenadas em posições de um vetor calculadas com base em funções hashing.

Funções Hash

Um exemplo de função hash pode ser aquele que leva em consideração o resto de uma divisão para definir a posição na estrutura de dados. Porém uma função hash não apresenta uma fórmula definida, e deve ser projetada levando-se em consideração o tamanho do conjunto de dados, seu comportamento e os tipos de dados-chave utilizados.

As funções hash são o cerne na construção das tabelas hashing, e o desenvolvimento de uma boa função de hash é essencial para que o armazenamento dos dados, a busca e o tratamento de colisões (assunto abordado no próximo tema) ocorram de forma mais eficiente possível. Uma boa função hash, em suma, deve ser:

Fácil de ser calculada. De nada valeria termos uma função com cálculos tão complexos e lentos que todo o tempo que seria ganho no acesso a informação com complexidade 𝑂(1), seria perdido calculando uma custosa função de hash;

Capaz de distribuir palavras-chave o mais uniforme possível;

Capaz de minimizar colisões. Os dados devem ser inseridos de uma forma que as colisões sejam as mínimas possíveis, reduzindo o tempo gasto resolvendo colisões e também reavendo os dados;

Capaz de resolver qualquer colisão que ocorrer;

O método da divisão

Um tipo de função hash muito adotada é o método da divisão, em que dividimos dois valores inteiros e usamos o resto dessa divisão como a posição desejada.

Quando nossas palavras-chave são valores inteiros, dividimos o número pelo tamanho do vetor e usamos o resto dessa divisão como a posição a ser manipulada na tabela hashing. Caso uma palavra-chave adotada seja um conjunto grande de valores inteiros (como um número telefônico ou CPF por exemplo), poderíamos somar esses valores agrupados (em pares ou trios) e também dividir pelo tamanho do vetor, obtendo o resto da divisão.

De modo geral, quando precisamos mapear um número de chaves em m espaços (como os de um vetor) pegando o resto da divisão entre ambos, chamamos isso de método da divisão. Esse método é bastante rápido, uma vez que requer unicamente uma divisão. ℎ(𝑘) = 𝑘 𝑀𝑂𝐷 𝑚

Existem alguns valores de m que devem ser minuciosamente escolhidos para não gerar povoamentos de tabelas hash ruins. Por exemplo, utilizar 2 ou múltiplos de 2 para o valor de m tende a não ser uma escolha. Isso porque o resto da divisão por dois, ou qualquer múltiplo seu, sempre resultará em um dos bits menos significativos, gerando um número bastante elevado de colisões de chaves.

Em hash precisamos trabalhar com números naturais para definir as posições na tabela, uma vez que linguagens de programação indexam as estruturas de dados (como vetores e matrizes) usando esse tipo de dado numérico. Desse modo, precisamos que nossas chaves sejam também valores naturais. Caso não sejam, precisamos encontrar uma forma de transformá-las para que sejam.

Para chaves com caracteres alfanuméricos, podemos adotar a mesma Equação, fazendo pequenas adaptações. Convertemos os caracteres para números decimais seguindo uma codificação (tabela ASCII, por exemplo), somamos os valores, dividimos pelo tamanho do vetor e obtemos o resto da divisão como posição de inserção da palavra-chave na tabela hashing.

Adotar números primos, especialmente aqueles não muito próximos aos valores de potência de 2, tende a ser uma boa escolha para o tamanho do vetor com palavras-chaves alfanuméricas.

Por fim, quando trabalhamos com valores-chave sendo conjuntos de caracteres, devemos tomar cuidado com palavras que contenham as mesmas letras, mas em ordens diferentes (anagrama). Por exemplo, uma palavra-chave com quatro caracteres chamada ROMA poderá gerar o mesmo resultado que uma palavra-chave chamada AMOR, pois os caracteres são os mesmos rearranjados de outra maneira. Uma função de hash deve ser cuidadosamente definida para tratar este tipo de problema caso ele venha a ser recorrente; caso contrário, teremos excessivas colisões.

O método da multiplicação

Esse método de construção de funções hash funciona da maneira que, primeiro, multiplicamos a chave k por uma constante A. Essa constante deve estar em um intervalo 0 < 𝐴 < 1 e extrair a fração de kA. Em seguida, multiplicamos esse valor por m e arredondamos o resultado para baixo. ℎ(𝑘) = ⌊𝑚(𝑘 𝐴 𝑀𝑂𝐷 1)⌋

Esse método apresenta como desvantagem o fato de ser mais lento para execução em relação ao método da divisão, pois temos mais cálculos envolvidos no processo, porém tem a vantagem de que o valor de m não é crítico, não importando o valor escolhido.

Em contraponto ao método de divisão, normalmente adotamos um múltiplo de 2 para seu valor, devido à facilidade de implementação. A constante A, embora possa ser qualquer valor dentro do intervalo 0<A< 1, é melhor com alguns determinados valores. Segundo Knuth (1998), um ótimo valor para essa constante é A=(√5−1)/2≅0,618.

Hashing universal

Considerando que uma chave k qualquer tem a igual probabilidade de ser inserida em qualquer uma das posições de um vetor, em um pior cenário seria possível que um conjunto de chaves a serem inseridas caiam sempre na mesma posição do vetor, caso utilizem a mesma função hash h(k). Portanto a complexidade para a inserção nessa hash será 𝑂(𝑛). Podemos evitar esse tipo de problema escolhendo uma função hashing aleatoriamente dentro de um universo H de funções. A esta solução chamamos de hashing universal.

Na hashing universal, no início da execução de um algoritmo de inserção, sorteamos aleatoriamente uma função de hash dentro de uma classe de funções cuidadosamente desenvolvida para a aplicação desejada. A aleatoriedade evita que qualquer entrada de dado resulte no pior caso. É bem verdade que a aleatoriedade poderá nunca resultar em um caso perfeito, em que nenhuma colisão ocorre, mas teremos sempre uma boa situação média.

Existe outro método bastante conhecido de implementação de hash universal que emprega matrizes aleatórias.

Tabela Hashing de endereçamento aberto e tentativa linear

A tabela hash pode ser implementada de diferentes formas. A implementação impacta diretamente em como os dados são inseridos e no tratamento das colisões de hashs.

Podemos desenvolver uma tabela hashing por meio de uma implementação utilizando endereçamento aberto. Nesse tipo de implementação, a tabela é um vetor de dimensão m e todas suas chaves são armazenadas no próprio vetor. O endereçamento aberto é bastante empregado quando o número de hashs a serem armazenadas é pequeno se comparado com o tamanho do vetor.

É possível implementá-la utilizando uma estrutura heterogênea do tipo registro, em que temos como campos um valor para ser usado como palavra-chave, podendo ser um inteiro ou alfanumérico, por exemplo. E temos também um campo que mantém o status daquela posição, representando se ele está livre, ocupado por uma chave ou se a chave daquela posição já foi removida.

Colisões: quando uma palavra-chave deve ser posicionada em um espaço do vetor em que já está ocupado.

Na tentativa linear, sempre que uma colisão ocorre, tenta-se posicionar a nova chave no próximo espaço imediatamente livre do vetor.

Caso o algoritmo de tentativa linear fique buscando uma posição vazia indefinidamente até chegar ao final do vetor e não a encontre, ele retorna ao início e busca até voltar à posição inicialmente testada. Caso nenhum local livre seja localizado, a palavra-chave não pode ser inserida.

Para a tentativa linear, todas as funções de manipulação da tabela de hash (inserção, remoção e busca de um elemento) apresentam risco de colisão para cada tentativa de manipulação.

Embora essas funções apresentem no melhor caso complexidade constante, não podemos garantir que elas terão sempre esse tempo, uma vez que o risco de colisão é sempre iminente, independentemente da operação.

Além disso, a tratativa linear funciona com agrupamentos primários de dados, ou seja, podem ocorrer longos trechos de endereços ocupados em sequência. Como a tentativa linear testa um elemento por vez, sequencialmente, a complexidade para o pior caso sempre será 𝑂(𝑛) para todas as funções apresentadas (inserção, busca e remoção).

Tabela Hashing de endereçamento aberto e tentativa quadrática

Na tentativa quadrática, sempre que uma colisão ocorre, tenta-se posicionar a nova chave no próximo espaço que está d posições de distância do primeiro testado, em que 1 ≤ 𝑑 ≤ 𝑇𝐴𝑀𝐴𝑁𝐻𝑂_𝑉𝐸𝑇𝑂𝑅.

A análise para o pior case da tentativa quadrática não difere da tentativa linear. A inserção, busca e remoção apresenta complexidade BigO 𝑂(𝑛). Este método acaba por ser mais eficiente em tempo de execução somente para situações de casos médios.

Tabela Hashing com endereçamento em cadeia

Podemos implementar uma tabela hashing empregando conceitos de listas encadeadas. Nesse cenário, temos também um vetor de dimensão m para representar a tabela, porém cada posição do vetor armazenará um endereço para o início de uma lista encadeada, de forma semelhante ao que trabalhamos na construção de uma lista de adjacências em grafos.

A forma como as colisões são tratadas por esse tipo de endereçamento é diferente. Nele, não é necessário encontrarmos uma nova posição no vetor para alocarmos o elemento colidido. Basta inseri-lo na mesma posição calculada, mas como mais um elemento da lista encadeada simples. A inserção é dada sempre antes do Head.

Note que, sempre que necessário buscar uma chave desse vetor, basta recalcular a posição usando a função hashing e, em seguida, varrer a lista encadeada simples daquela posição até localizar a palavra-chave correspondente.

A complexidade para o endereçamento de cadeia apresenta tempo constante para o pior caso 𝑂(1) para a inserção na tabela. Esse valor é constante, pois a inserção consiste somente em calcular a função hashing e inserir no Head da lista da posição correspondente, sem a necessidade de varredura da lista nem de tratamento de colisões.

Para a remoção da lista, o pior cenário seria a necessidade de varrer uma lista encadeada de uma posição buscando um elemento que está na última posição dessa lista simplesmente encadeada. Portanto, a complexidade está atrelada ao número de palavras-chave (números de elementos) de cada lista encadeada, resultando em 𝑂(𝑛).